How to Format Math and Equations

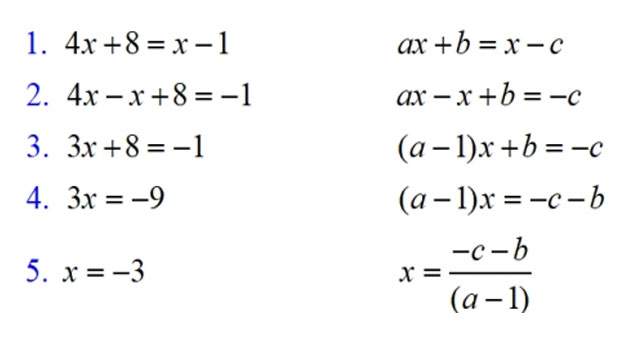
At ProofreadingPal, we’re often tasked with proofing academic and professional math and science documents. Projects of this kind are likely to feature equations and formulas. We expect a great deal of math in papers on the physical sciences, but formulas can show up in any subject that uses statistical analysis, including economics, sociology, history, and even literature.

The way we edit these passages is a little different from how we handle prose. Generally, we are not expected to check the math for accuracy because, to be practical, we don’t match editors to clients according to academic background, and to be ethical, that would be crossing the line from editing to co-authorship.

So our interest is, as always, with grammar and syntax. If mathematics is (as is often said) a language, then a formula or equation is analogous to a sentence. Simple equations can easily be expressed in words. “Two plus two equals four,” for instance, is a grammatically correct sentence; you could diagram it like any other. But we don’t get many papers with that particular equation.

Let’s look at some of the conventions that govern mathematical grammar at all levels.

Equations as Sentences

In a mathematical expression, numbers, variables, and operators act like the parts of speech. Numbers and variables are nouns; operational symbols may variously act as conjunctions, adverbs, adjectives, prepositions, or transitive verbs. As with words in the sentence, the symbols in a mathematical expression should be separated by a single space, as shown below.

There are a couple of important exceptions. When the operational symbol is actually a part of the numeral or variable, as in the case of negative numbers (e.g., –1), no space is inserted. And when multiplying variables, the multiplication sign is usually omitted altogether; placing the variables next to one another with no intervening space serves to indicate the multiplication function. As shown in the example below, this convention is useful as a way to avoid excessive use of parentheses to separate discrete mathematical operations.

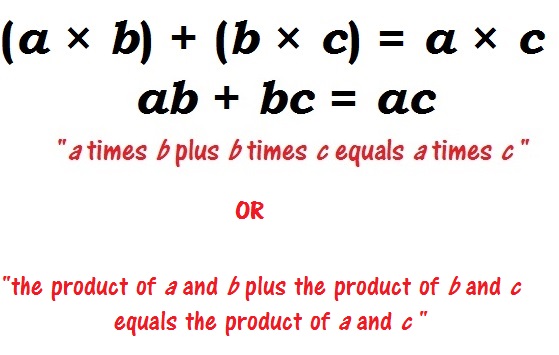
Note the multiplication symbol in the example. It’s a different character from the lowercase letter X, and the two should not be used interchangeably. Neither should you use a hyphen to indicate subtraction. You can find the plus (+), equals (=), and division (/) operators on a standard keyboard; for the multiplication (×), subtraction (–), and other operators, click over to the Insert tab and check the Symbol menu on the far right. Using the correct symbols in an equation is as important as properly spelling the words of a sentence.

Equations in Sentences

Brief or incidental mathematical expressions can be integrated right into the body text: “Einstein’s theory of general relativity is expressed as E = mc², where E represents energy, m stands for mass, and c is the constant speed of light.” Expressions critical to understanding the content of the paper should appear on a separate line, usually indented by a half-inch. Even when a line of text is interrupted in this way, though, punctuate appropriately. An expression that appears on a separate line may still be part of a sentence that begins on the line above and ends on the line below, as shown here.

Letters as Numbers

A variety of symbols can stand for variables, constants, and functions in mathematical expressions. Some of these symbols do double duty as the twenty-six letters of the standard English alphabet. To avoid confusion, then, alphabetic variables should always be italicized, whether they appear in the inline text or on a separate line.

Mathematical expressions may occasionally include functions expressed in words or abbreviations of words. These letters must not be italicized. For example, “cos A,” with “cos” set in Roman type, indicates the cosine of angle A, while cos, set in italics, would indicate the product of the three variables c, o, and s all multiplied together—quite a different proposition!

Other symbols should generally not be italicized, such as Arabic numerals, Greek letters, script, and double-struck characters.

Layout and Numbering

Some academic styles require important mathematical expressions to be numbered for reference, much like figures and tables. For proper formatting, keep the equation left-aligned; indent by a half-inch; and after the equation, enter the relevant reference number, enclosed in parentheses, close to the right-hand margin. Use the tab key to achieve proper alignment.

Subsequent mentions of this equation appear in the text such as “This principle is demonstrated in equation (3).”

Further Reading

These few simple rules form the foundation for clear, readable presentation of formulae and equations in academic writing. Chapter 12 of the Chicago Manual of Style and chapter 6 of the Publications Manual of the American Psychological Association are excellent resources for further reading.

Jack F.